PiotrFest 2024

I will discuss two results on the Planar Circular Restricted 3-Body Problem. Both results are computer assisted, but they are obtained with very different approaches. The first result is almost a quarter of a century old, but it is very appropriate to this conference, since it is one of the first applications I made of the computer assisted techniques developed by the Polish school. It concerns the existence periodic solutions and symbolic dynamics in the case Copenhagen case (primaries with equal masses). The second result (in collaboration with Jason Mireles James) is recent and it is obtained with a fixed point technique. It concerns the existence of branches of ejection-collision orbits (trajectories starting from one primary and ending in the other primary) with respect to either the mass ratio, or the energy, and bifurcations of such branches.

I will present results on the existence of periodic orbits for the nonautonomous Chafee-Infante equation:

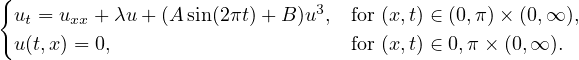The proofs are computer-assisted and based on interval arithmetic and rigorous integration of dissipative systems. Moreover, for the Chafee-Infante equation, we prove that the periodic orbits are locally attracting. We employ a new method of C¹ computations based on rigorous integration of unbounded sets.

When studying random dynamical systems described by stochastic differential equations, Lyapunov exponents are powerful tools to measure qualitative behavior. Moments Lyapunov exponents capture finer information, such as fluctuations of finite time Lyapunov exponents, and yield large deviations estimates. These moments Lyapunov exponents can be obtained as principal eigenvalues of elliptic PDEs associated to the original SDEs. I will describe a computer-assisted approach that can be used to obtain rigorous enclosures of such eigenvalues. This is joint work with Alex Blumenthal (Georgia Tech), Maximilan Engel (U. of Amsterdam) and Alexandra Blessing-Neamtu (U. of Konstanz).

In this talk I will present a computer-assisted method which allows to perform long (rigorous) integrations in Parabolic PDEs with periodic boundary conditions in space. The method is based on an expansion of the solution in Fourier series in space and Chebyshev polynomials in time. Mixing Fourier series and Chebyshev polynomials generates tridiagonal infinite matrices which complicate the computer-assisted analysis in coefficients space, compared to the diagonal structure in Fourier series alone. I will show how such operators actually produce decay in the coefficients and how this allows to increase the time of integration. The resolution of an initial value problem in the Swift-Hohenberg PDE will be presented as an illustration.

Blenders originally emerged as objects in dynamical systems as an example given by C. Bonatti and L. Díaz of a system which is not uniformly hyperbolic but it is robustly transitive. Roughly speaking, on an n-manifold, a blender is a hyperbolic invariant subset of the system that allows for robust intersections of s-dimensional stable manifolds and u-dimensional unstable manifolds, with s + u < n. The way to make this intersection robust without "the right dimensions" is to make the stable set of the blender to "fill the space as if it is higher dimensional". This intersection allows the existence of robust heterodimensional cycles and gives conditions for robust transitivity. We present a family of D.A. (derived-from-Anosov) systems on the 3-torus for which we are exploring the presence of blenders, using computer aided strategies. This is ongoing work made with the collaboration of Andy Hammerlindl and Warwick Tucker.

We demonstrate a recent proof, based on joint work with Rafael Ramírez, of chaos in billiards inside circular polygons. Circular polygons are closed plane curves obtained by concatenating a finite number of circular arcs so that, at the points where two arcs meet, the tangents agree. The resulting curves are strictly convex and C¹, but not C². We prove that there is a set accumulating on the boundary of the domain in which the return dynamics is semiconjugate to a transitive shift on infinitely many symbols. As a result, this return map has infinite topological entropy, and the billiard has many periodic orbits of large period. In addition, there are billiard orbits along which the sequence of angles of reflection tends to 0 with optimal speed. The proof uses a technique that is equivalent to the method of correctly aligned windows.

We study the global instability of dynamical systems on complex lattices by shadowing chains of nontransversal heteroclinic connections between several periodic orbits. The systems we consider are inspired by the so-called toy model systems (TMS) used to show the existence of energy transfer from low to high frequencies in the nonlinear cubic Schrödinger equation (NLSE) or generalizations. Using the geometric properties of the complex projective space as a base space, we show how to generate in a natural way a large collection of systems containing these chains, both in the Hamiltonian and non-Hamiltonian setting. On the other hand, we characterize the property of "block diagonal dynamics along the heteroclinic connections" that allows these chains to be shadowed, a property which in general only holds for transversal heteroclinic connections. Due to the lack of transversality, only finite chains are shadowed, as there is a dropping dimensions mechanism in the evolution of any disk close to them. The main shadowing tools used in our work are the covering relations as introduced by Piotr Zgliczynski.

This is a joint work with Piotr Zgliczynski of the Jagiellonian University in Krakow.

We introduce a three-step method to construct on a simplicial complex a combinatorial dynamical system in the sense of Forman from vector field data by means of a linear minimization problem, where the solution to this problem induces an admissible matching for the combinatorial dynamical system. We show that the constraint matrix of the minimization problem is unimodular, allowing us to relax the problem from binary-valued to real-valued and permitting its resolution in polynomial time for the number of simplices. We demonstrate the effectiveness of the method on the Lotka-Volterra model and on the Lorenz attractor model. We also describe three potential extensions to our method : how barycentric subdivision can be applied to the simplicial complex to increase the resolution and obtain a solution that better fits the underlying dynamics of the data, how to add constraints to the minimization problem to fix the number of critical simplices, and how to add constraints to obtain a solution that induces a gradient matching.

In this talk, we consider the existence of partially hyperbolic invariant tori with Diophantine frequencies and their invariant bundles in periodic and quasi-periodic analytic Hamiltonian systems. We present an a-posteriori KAM theorem stating that if we have embeddings for the torus and its stable bundle satisfying that the error in their functional invariance equations is small enough, then there is an invariant torus with stable and unstable invariant bundles nearby. The method of proof is based on the parameterization method and consists on constructing an iterative procedure that defines sequences of embeddings that converge to solutions of their invariance equations in a complex strip of the torus. In particular, we obtain both the stable and unstable bundles simultaneously and the application of the theorem to autonomous Hamiltonian systems is straightforward. The results rely on the geometrical properties of the system and of invariant tori and do neither assume action-angle coordinates nor a perturbative setting. Additionally, the theorem is constructed to be suitable for numerical implementations and computer assisted proofs. Non-rigorous implementations have been applied to compute 3-dimensional invariant tori in the Elliptic Restricted Three Body Problem.

In this talk we present an a-posteriori KAM theorem for the existence of Lagrangian invariant tori in Hamiltonian systems of n degrees of freedom. We present a (modified) quasi-Newton method for the invariance equation of the torus parameterization, whose convergence from an initial approximation, and under appropriate non-degeneracy conditions, leads to the proof of the result with optimal estimates. The approach is suitable for developing numerical algorithms and performing computer-assisted proofs.

All these will be put in context with actual results in the Sun-Jupiter-Saturn system and its comparison with previous results in other scenarios, and its connections with computer-assisted proofs and fast-and-accurate estimates using rigorous FFT.

This is joint work with Alex Haro (Universitat de Barcelona-CRM).

The existence of periodic windows in the parameter space is a common feature of nonlinear systems capable to produce chaotic behavior. Detection of positions of periodic windows is important both from the theoretical and practical points of view. In this work, we study and prove the existence of periodic windows for the Rössler system. The proposed method is a combination of the symbolic dynamics based approach to find unstable periodic orbits, the continuation method to calculate positions of periodic windows and interval arithmetic tools to prove their existence. The existence of several thousands of periodic windows close to the classical parameter values is proved and periodic attractors very close in the parameter space to the Rössler attractor are found.

A motivation for this work is the system consisting of Sun, Jupiter, the Trojan asteroid (624) Hektor, and its moonlet Skamandrios. The asteroid Hektor is located near the Lagrangian point L4 of the Sun-Jupiter system, and has an irregular shape. The motion of the moonlet Skamandrios is close to spin-orbit resonance, so a small perturbation could potentially lead to ejection of the moonlet or to collision with the asteroid. Additionally, the elliptic orbit of Jupiter has a periodic forcing effect on the motion of the moonlet.

We focus on the planar elliptic restricted four-body problem as a simplified model for this system. We derive the corresponding elliptic Hill four-body problem, representing the limiting case when the mass of the asteroid tends to zero while Sun and Jupiter are sent to infinity. The resulting system can be viewed as a small perturbation of the circular Hill four-body problem, with the perturbation parameter being the eccentricity of Jupiter’s orbit. We show that the effect of the perturbation can accumulate and give rise to some orbits whose energy undergoes significant changes over time. Consequently, there is a theoretical possibility that the moonlet can be ejected or crash onto the asteroid.

We present a constructive solution method of some (retarded or advanced) equations.

We assume that the equation is formally close to an ODE and that the ODE admits hyperbolic solutions (that is, perturbations transversal to a trajectory grow exponentially either in the past or in the future) and we show that there are solutions of the functional equation close to these hyperbolic solutions of the ODE.

The proof does not require to formulate the delayed problem as an evolution for a class of initial data. The main result is formulated in an "a-posteriori" format and allows to show that solutions obtained by non-rigorous approximations are close (in some precise sense) to true solutions.

We discuss some particular cases like small delays, neutral forms, and implicitly defined perturbations.

This is a joint work with R. de la Llave and J. Yang.

The Restricted 3-Body Problem models the motion of a body of negligible mass under the gravitational influence of two massive bodies, called the primaries. If the primaries perform circular motions and the massless body is coplanar with them, one has the Restricted Planar Circular 3-Body Problem (RPC3BP). In rotating coordinates, it is a two degrees of freedom Hamiltonian system with five critical points, L₁,..,L₅, called the Lagrange points. The Lagrange point L₃ is a saddle-center critical point (collinear with the primaries and beyond the largest one) with a 1-dimensional stable and unstable manifold. When the ratio between the masses of the primaries μ is small, the modulus of the hyperbolic eigenvalues are weaker, by a factor of order 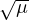, than the elliptic ones.

The first result we present is an asymptotic formula for the distance between the stable and unstable manifolds of L₃. Due to the rapidly rotating dynamics, this distance is exponentially small with respect to 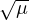and, as a result, classical perturbative methods (i.e the Melnikov-Poincaré method) can not be applied.

The second result studies the family of Lyapunov periodic orbits of L₃ with Hamiltonian energy level exponentially close (with respect to 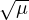) to that of L ₃. In particular, we show that there exists a set of periodic orbits whose unstable and stable manifolds intersect transversally. By the Smale-Birkhoff homoclinic theorem, this implies the existence of chaotic motions (Smale horseshoe) exponentially close to L₃ and its invariant manifolds. In addition, we also show the existence of a generic unfolding of a quadratic homoclinic tangency which leads to the existence of Newhouse domains for the RPC3BP.

This is a joint work with Inma Baldomá, Maciej J. Capiński and Marcel Guardia.

In this talk I will explain a recent result about the existence of transfer of energy orbits in a chain of infinitely many weakly coupled pendulums. This is a Hamiltonian system posed on an infinite lattice with formal or convergent Hamiltonian. We develop geometric and functional tools to perform an Arnold diffusion mechanism in infinite dimensional phase spaces. In this way we construct solutions that move the energy of the pendulums along any prescribed path in the lattice. This is a joint work with Filippo Giuliani.

In this talk, we present evidence of the stability of a simplified model of our Solar System, a flat (Newtonian) Sun-Jupiter-Saturn system with realistic data, that is, with masses of the Sun and the planets, their semi-axes, eccentricities, and precessions of the planets close to the real ones. The evidence is based on convincing numerics that a KAM theorem can be applied to the Hamiltonian equations of the model to produce quasi-periodic motion, that lies in an invariant torus, with the appropriate frequencies.

To do so, first KAM schemes to compute translated tori are used to continue from the Kepler approximation (two uncoupled two-body problems) up to the actual Hamiltonian of the system, for which the translated torus is invariant tori. Second, KAM schemes for invariant tori are used to refine the solution of the invariant equations giving the invariant torus. Last, the convergence of the KAM scheme for the invariant torus is (numerically) checked by applying several times a KAM iterative lemma, from which we obtain that the final torus (numerically) satisfies the existence conditions given by a KAM theorem.

This is a joint work with Jordi-Lluís Figueras (Uppsala University).

In this talk we will explore the Poincaré scenario for delay differential equations (DDEs), that is the transverse intersection of the stable and unstable manifolds of a periodic orbit. We introduce an implicit discrete dynamical system that inherently reflects the dynamics of the original DDE. Within this new framework, we develop a shooting method from the unstable manifold to the stable one. By applying a Newton-Kantorovich type theorem, we demonstrate the conditions under which a transverse intersection of these manifolds occurs.

In this talk we consider the Rössler equations [o.e. rössler, An equation for continuous chaos, Phys. Lett. 57A (1975), 397–398] in ℝ³

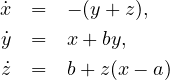
Inspired by the numerical studies and by the theory of isotopy stability for surface homeomorphisms, we consider a certain heteroclinic condition – which, when imposed on the equations above, forces the existence of infinitely many periodic trajectories. Following that, we use Template Theory and Orbit Index Theory to first study the topology of these periodic trajectories, and then study their persistence under perturbations in the parameter space. Time permitting, we will also prove how one can use these results to rigorously reduce the flow to a one-dimensional model: the quadratic family – which we do by explicitly matching the flow dynamics and polynomial dynamics based on their shared periodic dynamics. Finally, we tie all these results together and conjecture how they describe the evolution of the Rössler attractor from order into chaos.

In this talk we present current work on developing a computer assisted proof for the stability of pulse solutions to the Swift-Hohenberg equation, generalizing the framework based on counting conjugate points / the Maslov index developed in Beck & Jaquette (2022). We have made significant theoretical advancements to this end, needed to account for essential degeneracies, however more work remains on the CAP front.

The general set up is to first compute a homoclinic orbit of a 4D Hamiltonian ODE. Next one evolves unstable vector bundles of the linearized system from one end of the homoclinic to the other. These vector bundles define a heteroclinic orbit in the space of Lagrangian Grassmanians (limiting from a point to a periodic orbit), and the number of conjugate points counts the number of times the heteroclinic orbit passes through a fixed reference frame. To get a validated count of the conjugate points, one must show that they only occur in a compact region, which requires a careful analysis of the limiting behavior of this path of Lagrangian subspaces, and the taming of external resonances in an application of the parameterization method.

This talk is based on joint work with Hannah Pieper and Margaret Beck.

In this talk I will summarize some recent results about the dynamics of a small particle in the vicinity of the Lagrangian points of the real Earth-Moon system. A first model is the classical Restricted Three-Body Problem (RTBP) that has been extensively studied in the literature, showing the existence of regions around the triangular points that require a huge time to escape from them. However, numerical simulations using high fidelity models for the Solar system show that particles escape from these regions after a few years. Moreover, there is observational evidence of clouds of dust near these points (known as Kordylewski clouds), which implies that some kind of stability must be present.

In the presentation I will discuss several intermediate models to account for the main perturbations on the RTBP model and how they affect its stability regions, showing a dynamical mechanism to explain the existence of these clouds.

The poster will present the main results of the paper that is joint work with Piotr Oprocha: "Graphs with tranches: consequences for topology and dynamics" arXiv:2405.05407 Tranches are non-degenerate elements of monotone decomposition of a continuum (such as the interval limit set in the topologist sine curve or Warsaw circle) We consider classes that generalize the concept of topological graphs, describe their topological structure and comment on how their structure restricts admissible dynamics.

A blender is a tool for proving that there is a new type of ‘wild’ chaotic dynamics in diffeomorphisms of dimension at least three and vector fields of dimension at least four, which is characterised by the robust existence of heterodimensional cycles and homoclinic tangencies. More specifically, a blender is a hyperbolic set with the characterising property that its, say, stable manifold behaves like an object of a dimension larger than given by the number of (locally) contracting directions.

For the lowest-dimensional case of a blender of a diffeomorphism, its one-dimensional stable manifold weaves through phase space in such a way as to be unavoidable by an open set of one-dimensional smooth curves; we speak of the carpet property. We show with two examples of explicitly given diffeomorphisms how this property can be checked via the computation of extremely long pieces of one-dimensional stable manifolds of relevant saddle points. In particular, this allows us to determine when a given hyperbolic set is a blender, when it is not, and how a blender may emerge or disappear. This type of geometric information may be used to inform subsequent computer-assisted proofs of the existence of a blender and of associated heterodimensional cycles.

This is joint work with Dana C’Julio, Sam Doak and Hinke M Osinga.

In this talk, we present a computational methodology for analyzing the dynamics of compact delay maps derived from delay differential equations (DDEs) of the form y′(t) = αy(t) + g(y(t - τ)). Our approach integrates Chebyshev series expansions, the Fast Fourier Transform (FFT), and the Discrete Poisson Summation Formula to rigorously evaluate the delay map. Leveraging this rigorous evaluation, we develop a method to establish the existence of periodic orbits and determine their Morse indices. Furthermore, we provide a technique to rigorously enclose the unstable eigenvectors, which are essential for computing the unstable manifolds of periodic orbits in DDEs. We demonstrate the application of our framework using the Mackey-Glass equation as a case study.

For a mechanical system consisting of a rotator and a pendulum coupled via a small, time-periodic Hamiltonian perturbation, it is kwown that, under suitable explicit conditions, there exist orbits along which the energy of the rotator grows by an amount independent of the size of the coupling parameter, for all sufficiently small values of the coupling parameter. There is a vast literature on establishing Arnold diffusion for such systems.

In this talk, we present the case when an additional, dissipative perturbation is added to the rotator-pendulum system with coupling. Therefore, the system obtained is not symplectic but conformally symplectic.

We provide explicit conditions on the dissipation parameter, so that the resulting system has pseudo-orbits exhibiting energy growth.

Our approach is based in the study of the scattering map, which turns out to be a symplectic map, even if the system is not symplectic, but conformally symplectic.

Consider a one-parameter family of smooth surface diffeomorphisms unfolding a quadratic homoclinic tangency to a hyperbolic fixed point. It is well known that in this unfolding there exists a Newhouse domain, i.e. an open set of parameters (containing the critical one in its closure) for which the corresponding diffeomorphism exhibits persistent homoclinic tangencies. Moreover, in the last decades, quite a number of surprisingly exotic dynamical phenomena have been shown to exist for residual sets of parameters contained in the Newhouse domain.

The analysis of the unfolding is certainly more subtle when the homoclinic tangency is associated to a persistent degenerate saddle, i.e. a parabolic fixed point which exists for all values of the parameter and for which the topological picture of the local dynamics resembles that of a hyperbolic fixed point (existence of invariant manifolds and C⁰ Lambda lemma). These degenerate saddles appear naturally in several models in Celestial Mechanics, in particular, in the so-called restricted 4 Body Problem. We prove that, in a particular configuration of the latter model which can be reduced to an area preserving map, there exist Newhouse domains associated with the unfolding (as we move the masses of the bodies) of a quadratic tangency of a degenerate saddle. As a consequence we obtain the existence of a set of masses for which there exist hyperbolic sets of Hausdorff dimension arbitrarily close to 2 which are accumulated by elliptic islands. Similar results have been obtained by Gorodetski and Kaloshin using different techniques. This is joint work with J.M.Garrido and J. Paradela

The Borel transform can be used to study functional equations whose solutions are C infinity but not analytic. Such equations describe invariant manifolds attached to parabolic fixed points and the solution of heat type equations. A fundamental challenge in working with the Borel transform is that it turns products into complex convolutions. This work aims to develop validated numerical methods for complex convolutions which can then be used in computer assisted proofs involving the Borel transform.

I will talk about validated computations for stable and unstable manifolds attached to periodic orbits for a class of compact, infinite dimensional, discrete time dynamical systems called Delay Maps. These maps correspond to time tau maps for certain delay differential equations. Since the maps are compact, the unstable manifold is finite dimensional and can be studied using the parameterization method. The stable manifold has finite co-dimension, and other tools are needed. I’ll discuss a stable manifold theorem for these maps. One complication is that a periodic orbit for a delay map will always have eigenvalues on the unit circle, and these must be treated with care.

This is joint work with J.P. Lessard and Olivier Henot.

Motivated by the question "Can you hear the shape of a drum?" and spectral rigidity for metrics for an expanding circle map of degree at least 2, we define Lyapunov spectrum as the set of all Lyapunov exponents (multipliers) at periodic orbits. This set is analogous to the unmarked length spectrum of negatively curved metrics on surfaces of genus at least 2. Is the following local rigidity holds: every C r smooth expanding circle map f has a neighborhood (in C r topology) such that any perturbation of f within this neighborhood that keeps the Lyapunov spectrum must be smoothly conjugate to f (subject to some sparsity assumption on the spectrum on f )? The answer is positive. The proof uses a novel iterative scheme which we will outline in the talk.
This is joint work in progress with Kostya Drach.

I will discuss efforts to develop a systematic, computationally efficient framework in which to identify the global dynamics of ordinary differential equations.

We use interval arithmetic to perform an extensive top-down search for central configurations. At each step we bisect a box in the configurations space until a central configuration is either found or proven not to exist. The algorithm succeeds until it stumbles upon bifurcations or near-zero masses; those cases have to be dealt with differently.

The present-day methodology of persistent homology is dominated by the approach grounded in an algebraic decomposition theorem of persistence modules. However, the original approach by Edelsbrunner, Letscher, Zomorodian (2002) has a more geometric flavour. It is based on a birth-death pairing in an ordered sequence of cells of a simplicial complex, called a filter. A filter may be interpreted as a Morse function inducing a combinatorial dynamical system on the simplicial complex. All birth-death pairs of the filter may be captured by a sequence of simplifications or smoothing of the system. The smoothing is achieved by a sequence of cancellations of shallow birth-death pairs. In dynamical terms these shallow birth-death pairs are nearby critical cells joined by heteroclinic connection. Originally, not all birth-death pairs have to be shallow and some cancellations are needed to make other birth-death pairs shallow. This leads to a poset structure in the collection of birth-death pairs. The induced dynamical system together with the poset, called the depth poset, strengthens the persistence diagram as a tool in TDA which may provide a better insight into the shape of data.

Based on a project in progress with Herbert Edelsbrunner. In collaboration with Michał Lipiński and Manuel Soriano Trigueros.

The phase shift between a point on a stable periodic orbit and its return position following a perturbation is often used to characterise oscillatory systems. Such phase resets are common in biological applications and they are studied mathematically in terms of the associated isochron geometry. Each isochron is an codimension-one manifold defined as the set of points in the basin of attraction of the oscillator that all converge under the flow with the same phase. While methods exist to compute one- and even two-dimensional isochrons, the dimension of isochrons of biological models that motivate their computation are often much higher. We develop a high-precision computational method based on the numerical continuation of a multi-segment boundary value problem that is independent of the dimension of the oscillatory system. Our method relates any three parameters in a given phase reset; essentially, we compute two-dimensional slices in a high-dimensional parameter space. A classical choice, which was already used by Winfree in the 1980s, relates the phase of a point resulting from a perturbation with both the amplitude of, and phase in the cycle at which the perturbation is applied; in particular, the direction in which the perturbation is applied is kept fixed for such a slice. We are also interested in phase resets for which the perturbation angles vary to explore their behaviour in dependence on the influence of isochron geometry in terms of this larger parameter space.

This is joint work with Peter Langfield, Kyoung Lee and Bernd Krauskopf .

We provide numerical evidence of chaos and diffusion for an infinitesimal particle around the Earth-Moon (EM) triangular points in the Sun-Earth-Moon (SEM) system via numerical experiments showing both homoclinic and heteroclinic tangles of invariant 2-tori around EM L₄ in the planar Hill restricted 4-body problem (PHR4BP). The PHR4BP is a π-periodic perturbation of the planar circular restricted 3-body problem (PCR3BP) and is a Hamiltonian system with two and a half degrees of freedom. The PHR4BP depends on two parameters: the EM mass ratio, μ = 0.0122, and the EM synodic month in years, m = 0.0808. Viewing m as the parameter introducing the periodic forcing of the Sun, we continue m from m_EM = 0 to m_SEM = 0.0808. As the Sun’s forcing is a significant perturbation, the results presented differ from classical Melnikov methods and Arnold diffusion in which an integrable system is perturbed by a small parameter. Rather, we explore a realistic system–the Sun-Earth-Moon system–as a perturbation of the nearly integrable PCR3BP and find numerical evidence of chaos via homoclinic tangle between an invariant 2-torus, as well as diffusion via heteroclinic tangle between invariant 2-tori of increasing amplitude. The present strategy relies on the stability of EM L₄ being partially hyperbolic. Hence, it is important to note that this strategy is not suitable for arbitrarily small values of the perturbation 0 < m ≪ 1, as the bifurcation changing the stability of the periodic orbit replacing EM L₄–from elliptic to partially hyperbolic–does not occur until m ≈ 0.0407.

Consider the spatial restricted three-body problem, as a model for the motion of spacecraft relative to the Sun-Earth system. We focus on the dynamics near the equilibrium point L₁ located between the Sun and the Earth. We show that it is possible for the spacecraft to transition from an orbit that is nearly planar relative to the ecliptic, to a maximum inclination orbit, at zero energy cost.

We provide several explicit constructions of such orbits, and also develop an algorithm to design orbits that achieve the *shortest transition time*.

Our main new tool is the ‘Standard Scattering Map’ (SSM), a semi-analytical representation of the exact scattering map. The SSM can be used in many other situations, from Arnold diffusion problems to transport phenomena in applications.

In collaboration with Amadeu Delshams (UPC, Barcelona) and Marian Gidea (Yeshiva University, NY).

Recent data from the Gaia telescope (Gaia DDR3) has provided precise information on the positions and velocities of stars within the Milky Way and its nearby regions, including the Large Magellanic Cloud (LMC). This data has prompted the need for methods to identify key galactic features from a single snapshot. In this study, we introduce a new approach to identify these features from a single snapshot, validated through simulations where multiple snapshots are available.

Using position and velocity data of stars from simulated barred galaxies, we aim to identify its central bar and characterize its position, size, pattern speed, and density distribution, as well as to detect the presence and location of galactic arms. Our method involves applying combinatorial and topological data processing tools to the available stellar data. Importantly, our method can be applied to barred galaxies even when stellar mass information is unavailable.

The derived characteristics are used to model the potentials of the different galaxy components, which are then incorporated into a classical dynamical system model. We compare the resulting invariant manifolds of the model with the arms obtained from the simulations, aiming to advance our understanding of spiral arm formation. Specifically, we examine the invariant manifolds associated to the Lyapunov periodic orbits around the unstable equilibrium points located at each end of the galactic bar. These manifolds delineate the arms and rings of barred galaxies, facilitating the transport of matter between different regions of the galaxy.

We extend our analysis to data from the LMC, a barred galaxy known for its asymmetrical density distribution within its central region and also among its arms. By applying our techniques, we aim to identify its central bar, characterize its pattern speed and density distribution, and delineate its arms. These discerned features serve as the basis for analyzing the equations of motion governing the galactic model, wherein the detected potential components are incorporated. We investigate how the inhomogeneity of the bar leads to an asymmetry in the galactic arms and examine the effects of the shifting observed in the LMC: the main bar axis is offset from the center of mass of the system.

Chaotic diffusion is commonly approached in the action domain, but its study in the frequency domain has advantages in quantifying chaotic phenomena, whether in cases of weak or strong chaotic motion. In this work, we use the frequency-space approach to study Atlas’ behaviour. The motion of the Saturninan moon is confined within a complex region of the phase space, which is located near the stochastic layer of the 54:53 Corotation Eccentric Resonance (CER) with Prometheus. In addition, the behavior in this region is complicated due to the overlap between the Prometheus-Atlas CER and the 70:67 Pandora-Atlas Mean Motion Resonance (MMR). In this dynamically intricate scenario, we investigate the stability of Atlas’ orbit choosing the frequency-space framework. Using the frequency analysis methods, we quantify chaotic diffusion for a broad number of initial conditions in the vicinity of Atlas’ current position in the phase space through the numerical integrations of the Saturn-Prometheus-Atlas (+Pandora) system. We obtained that Atlas’ orbit is mainly perturbed by Prometheus. The addition of Pandora turns the dynamical neighborhood of Atlas from a weakly chaotic regime (δ_tf((t) ~ 10^-3) to a moderately chaotic one (δ_tf((t) ~ 10^-2), but only slightly affects Atlas’ motion, which is slowly diffusing (δ_tf((t) ~ 10^-3), confined in the low-eccentricity regions of the phase space, not reaching strongly chaotic ones (δ_tf((t) ≥ 10^-1). This dynamical architecture prevents catastrophic events such as ejections or collisions with other bodies of the system, deeming it long-term stable.

We present an algorithm for a rigorous computation of lower bounds on the Hausdorffdimensions of Julia sets for a wide class of holomorphic maps. We apply this algorithm to obtain lower bounds on the Hausdorff dimension of the Julia sets of some infinitely renormalizable real quadratic polynomials, including the Feigenbaum polynomial p_Feig(z) = z² + c_Feig . In addition to that, we construct a piecewise constant function on [-2,2] that provides rigorous lower bounds for the Hausdorff dimension of the Julia sets of all quadratic polynomials p_c(z) = z² + c withc ∈ [-2,2]. Finally, we verify the conjecture of Ludwik Jaksztas and Michel Zinsmeister that theHausdorff dimension of the Julia set of a quadratic polynomial p_c(z) = z² + c, is a C¹-smooth function of the real parameter c on the interval c ∈ (c_Feig,-3∕4). This is joint work with Artem Dudko and Igors Gorbovickis.

We note that an attractor of a diffeomorphism subject to a bounded noise is an invariant open set which is completely determined by its boundary. When this boundary is smooth, it can be computed as a projection of a Legendrian invariant manifold of a certain deterministic map which preserves a contact structure. We use these observations to show that attractors with normally-hyperbolic boundaries depend continuously on small perturbations of the system.

Travelling waves form a prominent feature in the dynamics of scalar reaction-diffusion equations on unbounded cylinders. A topological invariant, based on a Floer homology construction, gives insight into the structure of the solutions of the reaction-diffusion equations. It encodes relations between connecting orbits on the one hand and equilibria, enhanced with (relative) index information, on the other. This leads to forcing theorems for travelling wave solutions. These theorems can be made effective by finding equilibria and their indices through computer-assisted proofs.

I will present several applications of some algorithms developed by Piotr Zgliczyński and his collaborators [1,2,3,4]. These algorithms, implemented as a part of the CAPD library [5], provide a general framework for rigorous numerical analysis of dynamical systems. I will show, that within this framework, some older and quite recent results obtained using different methods can be reproduced with little effort.

1. P. Zgliczyński, C1-Lohner algorithm, FoCM. (2002) 2:429-465
2. D. Wilczak, P. Zgliczyński, Cr-Lohner algorithm, Schedae Informaticae, Vol. 20 (2011), 9-46.
3. I. Walawska, D. Wilczak, An implicit algorithm for validated enclosures of the solutions to variational equations for ODEs, Appl. Math. Comp., Vol. 291C (2016), 303-322.
4. T. Kapela, D. Wilczak, P. Zgliczyński, Recent advances in rigorous computation of Poincarè maps, CNSNS, Volume 110, July 2022, 106366.
5. T. Kapela, M. Mrozek, D. Wilczak, P. Zgliczyński, CAPD::DynSys: a flexible C++ toolbox for rigorous numerical analysis of dynamical systems, CNSNS, Volume 101, October 2021, 105578.

We consider a collision singularity in the planar n-body problem. It is known that the normalized configuration curve must converge to the set of normalized central configurations (nCC). However, every nCC determines a circle of rotationally equivalent normalized configurations. One can imagine that by means of an infinite spin, a total collision solution could converge to such a circle instead of to a particular point on it. Here we prove that this is impossible for partial collisions, at least if the limiting circle of central configurations is isolated from other circles of central configurations. (it is believed that all central configurations are isolated, but this is not known in general). Our result generalizes recent theorem of Moeckel and Montgomery (arXiv:2302.00177), where total collision case was treated. Our proof builds on their approach, which used the center manifold theorem and Lojasiewicz inequality. Our contribution is in analysis of influence of other bodies on the colliding cluster and a new shadowing argument close to the center manifold.